La suma se utiliza generalmente para encontrar la suma de la lista de números. Como los electrodomésticos de la vida cotidiana aumentan día a día, el uso para contar la suma del precio de cada artículo es necesario, la suma es ampliamente utilizada para ese propósito.
En este post, explicaremos la definición y la fórmula de la notación sigma junto con sus ejemplos resueltos.
¿Qué es la suma?
El término que se utiliza para denotar la adición de la lista de los números y representó la lista de números en una función junto con la notación griega sigma con el lugar inicial y final se conoce como la notación de suma.
Esta técnica se utiliza ampliamente en matemáticas y estadística para resolver los problemas de la varianza, la desviación estándar, la suma de cuadrados, la media, etc. Se denota por ∑ (sigma). He aquí la expresión general para resolver los problemas de suma.
Ai = A1 + A2 + A3 + … + An
Donde ∑ es la notación, Ai es la función, i = 1 es el valor inicial de la función, y n es el valor final de la función.
Leyes de notación sigma
Nombre de la regla Regla
| Nombre de la regla | Regla |
| Ley de la constante | k = n * k |
| Ley de la suma | fi + qi = fi + qi |
| Ley de la diferencia | fi – qi = fi – qi |
| Ley del producto | fi * qi = fi * qi |
| Ley del cociente | fi / qi = fi / qi |
Cómo resolver los problemas de suma?
A continuación se presentan dos técnicas para resolver los problemas de suma:
- Utilizando una sumatoria calculadora
- Utilizando el método manual
Aquí vamos a explicar brevemente los métodos anteriores.
Utilizando una calculadora de sumatorias
Una sumatoria calculadora de AllMath es una herramienta útil para resolver problemas de suma con pasos.
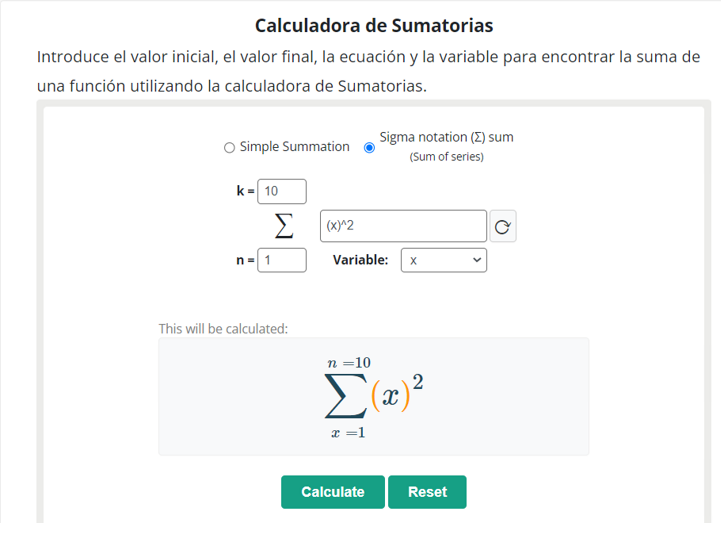
¿Cómo se utiliza esta calculadora?
Sigue los siguientes pasos.
- Selecciona el método como la suma simple o la notación sigma.
- Introduzca el valor inicial, la expresión y los valores finales en los campos de entrada requeridos.
- Seleccione la variable correspondiente «x» está seleccionada por defecto.
- Pulse el botón de calcular.
- La solución con los pasos aparecerá debajo del botón de calcular.
Utilizando el método manual
A continuación se presenta un método manual para resolver los problemas de suma. Vamos a calcular los problemas según los dos métodos para coger todo lo básico para resolver los problemas manualmente.
Ejemplo
Calcula el sumatorio de la función dada con el valor inicial 2 y el valor final 8.
f(u) = 3u4 + 12u3 – 19
Solución
Paso 1: En primer lugar, toma la expresión dada y aplícale la notación de la suma.
f(u) = 3u4 + 12u3 – 19
(3u4 + 12u3 – 19)
Paso 2: Ahora coloca el valor a la expresión dada desde la inicial hasta la final.
Para u = 2
3u4 + 12u3 – 19 = 3(2)4 + 12(2)3 – 19
3u4 + 12u3 – 19 = 3(16) + 12(8) – 19
3u4 + 12u3 – 19 = 48 + 96 – 19 = 125
Para u = 3
3u4 + 12u3 – 19 = 3(3)4 + 12(3)3 – 19
3u4 + 12u3 – 19 = 3(81) + 12(27) – 19
3u4 + 12u3 – 19 = 243 + 324 – 19 = 548
Para u = 4
3u4 + 12u3 – 19 = 3(4)4 + 12(4)3 – 19
3u4 + 12u3 – 19 = 3(256) + 12(64) – 19
3u4 + 12u3 – 19 = 768 + 768 – 19 = 1517
Para u = 5
3u4 + 12u3 – 19 = 3(5)4 + 12(5)3 – 19
3u4 + 12u3 – 19 = 3(625) + 12(125) – 19
3u4 + 12u3 – 19 = 1875 + 1500 – 19 = 3356
Para u = 6
3u4 + 12u3 – 19 = 3(6)4 + 12(6)3 – 19
3u4 + 12u3 – 19 = 3(1296) + 12(216) – 19
3u4 + 12u3 – 19 = 3888 + 2592 – 19 = 6461
Para u = 7
3u4 + 12u3 – 19 = 3(7)4 + 12(7)3 – 19
3u4 + 12u3 – 19 = 3(2401) + 12(343) – 19
3u4 + 12u3 – 19 = 7203 + 4116 – 19 = 11300
Para u = 8
3u4 + 12u3 – 19 = 3(8)4 + 12(8)3 – 19
3u4 + 12u3 – 19 = 3(4096) + 12(512) – 19
3u4 + 12u3 – 19 = 12288 + 6144 – 19 = 18413
Paso 3: Ahora toma la suma de todos los términos calculados anteriormente.
(3u4 + 12u3 – 19) = 125 + 548 + 1517 + 3356 + 6461 + 11300 + 18413
(3u4 + 12u3 – 19) = 41720
Alternativamente
Paso 1: En primer lugar, utiliza la ley de diferencia y suma de sigma y aplica la notación por separado a cada término de la función.
(3u4 + 12u3 – 19) = (3u4) + (12u3) – (19)
Paso 2: Ahora calcula cada término de la función por separado.
Para (3u4)
(3u4) = 3(2)4 + 3(3)4 + 3(4)4 + 3(5)4 + 3(6)4 + 3(7)4 + 3(8)4
(3u4) = 3(16) + 3(81) + 3(256) + 3(625) + 3(1296) + 3(2401) + 3(4096)
(3u4) = 48 + 243 + 768 + 1875 + 3888 + 7203 + 12288
(3u4) = 26313
Para (12u3)
(12u3) = 12(2)3 + 12(3)3 + 12(4)3 + 12(5)3 + 12(6)3 + 12(7)3 + 12(8)3
(12u3) = 12(8) + 12(27) + 12(64) + 12(125) + 12(216) + 12(343) + 12(512)
(12u3) = 96 + 324 + 768 + 1500 + 2592 + 4116 + 6144
(12u3) = 15540
Para (19)
(19) = 19 + 19 + 19 + 19 + 19 + 19 + 19
(19) = 19 x 7
(19) = 133
Paso 3: Escribe los resultados de las funciones sumatorias y encuentra su orden de operación de las mismas.
(3u4 + 12u3 – 19) = (3u4) + (12u3) – (19)
(3u4 + 12u3 – 19) = 26313 + 15540 – 133
(3u4 + 12u3 – 19) = 41853 – 133
(3u4 + 12u3 – 19) = 41720
Palabras finales
En este post, hemos cubierto toda la intención básica de la suma junto con ejemplos resueltos. Ahora eres testigo de que resolver los problemas de suma no es una tarea difícil. Usted puede resolver fácilmente los problemas de la suma, ya sea mediante el uso de una calculadora o el método manual discutido anteriormente.